Aprendiendo con la Física: junio 2017

martes, 27 de junio de 2017

El Radian

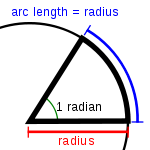
EL RADIÀN

El radián es la unidad de ángulo plano en el Sistema Internacional de Unidades. Representa el ángulo central en una circunferencia y abarca un arco cuya longitud es igual a la del radio. Su símbolo es rad. Hasta 1995 tuvo la categoría de unidad suplementaria en el Sistema Internacional de Unidades, junto con el estereorradián. A partir de ese año, y hasta el momento presente, ambas unidades figuran en la categoría de unidades derivadas.

Esta unidad se utiliza primordialmente en física, cálculo infinitesimal, trigonometría, goniometría, etc.

Un radián es la unidad de medida de un ángulo con vértice en el centro de un círculo cuyos lados son cortados por el arco de la circunferencia, y que además dicho arco tiene una longitud igual a la del radio.^{[cita requerida]}

El ángulo formado por dos radios de una circunferencia, medido en radianes, es igual a la longitud del arco que delimitan los radios dividida entre el radio; es decir, θ = s/r, donde θ es el ángulo, s es la longitud de arco, y r es el radio. Por tanto, el ángulo completo,

\scriptstyle {\theta }_{\text{circunferencia}}

, que subtiende una circunferencia de radio r, medido en radianes, es:

\theta _{\text{circunferencia}}={\frac {L_{\text{circunferencia}}}{r}}={\frac {2\pi r}{r}}=2\pi \ {\text{rad}}\,

El radián es una unidad sumamente útil para medir ángulos, puesto que simplifica los cálculos, ya que los más comunes se expresan mediante sencillos múltiplos o divisores de π.

{\rm {rpm={\frac {rev}{min}}={\frac {2\pi \ rad}{60\ s}}}}

Grados	0°	30°	45°	60°	90°	120°	135°	150°	180°	210°	225°	240°	270°	300°	315°	330°	360°
Radianes	0	π/6	π/4	π/3	π/2	2π/3	3π/4	5π/6	π	7π/6	5π/4	4π/3	3π/2	5π/3	7π/4	11π/6	2π

MOVIMIENTO CIRCULAR UNIFORME

Un cuerpo realiza un movimiento circular uniforme (m.c.u.) cuando su trayectoria es una circunferencia y su velocidad angular es constante. En este apartado vamos a estudiar:

El concepto de m.c.u. a través de las principales magnitudes cinemáticas presentes en él
Las características principales del m.c.u

CONCEPTO DE M.C.U.

La Naturaleza y tu día a día están llenos de ejemplos de movimientos circulares uniformes (m.c.u.). La propia Tierra es uno de ellos: da una vuelta sobre su eje cada 24 horas. Los viejos tocadiscos o un ventilador son otros buenos ejemplos de m.c.u.

El movimiento circular uniforme (m.c.u.) es un movimiento de trayectoria circular en el que la velocidad angular es constante. Esto implica que describe ángulos iguales en tiempos iguales. En él, el vector velocidad no cambia de módulo pero sí de dirección (es tangente en cada punto a la trayectoria). Esto quiere decir que no tiene aceleración tangencial ni aceleración angular, aunque sí aceleración normal.

CARACTERÍSTICAS DEL MOVIMIENTO CIRCULAR UNIFORME (M.C.U.)

Algunas de las principales características del movimiento circular uniforme (m.c.u.) son las siguientes:

La velocidad angular es constante (ω = cte)
El vector velocidad es tangente en cada punto a la trayectoria y su sentido es el del movimiento. Esto implica que el movimiento cuenta con aceleración normal
Tanto la aceleración angular (α) como la aceleración tangencial (at) son nulas, ya que la rapidez o celeridad (módulo del vector velocidad) es constante
Existe un periodo (T), que es el tiempo que el cuerpo emplea en dar una vuelta completa. Esto implica que las características del movimiento son las mismas cada T segundos. La expresión para el cálculo del periodo es T=2π/ω y es sólo válida en el caso de los movimientos circulares uniformes (m.c.u.)
Existe una frecuencia (f), que es el número de vueltas que da el cuerpo en un segundo. Su valor es el inverso del periodo

Velocidad tangencial. La frecuencia. Aceleraciòn centrìpeta.

VELOCIDAD TANGENCIAL:

La velocidad tangencial es igual a la velocidad angular por el radio. Se llama tangencial porque es tangente a la trayectoria.

La velocidad tangencial es un vector, que resulta del producto vectorial del vector velocidad angular ω por el vector posición r referido al punto P.

La velocidad tangencial es igual a la velocidad angular por el radio.

La velocidad tangencial, al igual que la velocidad angular, es constante.

LA FRECUENCIA:

Frecuencia una magnitud que mide el número de repeticiones por unidad de tiempo de cualquier fenómeno o suceso periódico.

Para calcular la frecuencia de un suceso, se contabilizan un número de ocurrencias de este teniendo en cuenta un intervalo temporal, luego estas repeticiones se dividen por el tiempo transcurrido. Según el Sistema Internacional (SI), la frecuencia se mide en hercios (Hz), en honor a Heinrich Rudolf Hertz. Un hercio es la frecuencia de un suceso o fenómeno repetido una vez por segundo. Así, un fenómeno con una frecuencia de dos hercios se repite dos veces por segundo. Esta unidad se llamó originalmente «ciclo por segundo» (cps).
Otras unidades para indicar frecuencias son revoluciones por minuto (rpm o r/min según la notación del SI); las pulsaciones del corazón se miden en latidos por minuto (lat/min) y el tempo musical se mide en «pulsos por minuto» (bpm, del inglés “beats per minute”).

1\,{\mathrm {Hz}}={\frac {1}{{\mathrm {s}}}}

Un método alternativo para calcular la frecuencia es medir el tiempo entre dos repeticiones (periodo) y luego calcular la frecuencia (f) recíproca de esta manera:

f={\frac {n}{T}}

donde T es el periodo de la señal.

ACELERACIÒN CENTRÌPETA

La aceleración centrípeta (también llamada aceleración normal) es una magnitud relacionada con el cambio de dirección de la velocidad de una partícula en movimiento cuando recorre una trayectoria curvilínea. Dada una trayectoria curvilínea la aceleración centrípeta va dirigida hacia el centro de curvatura de la trayectoria.

Cuando una partícula se mueve en una trayectoria curvilínea, aunque se mueva con rapidez constante (por ejemplo el MCU), su velocidad cambia de dirección, ya que esta es un vector tangente a la trayectoria, y en las curvas dicha tangente no es constante.

La aceleración centrípeta, a diferencia de la aceleración centrífuga, está provocada por una fuerza real requerida para que cualquier observador inercial pudiera dar cuenta de como se curva la trayectoria de una partícula que no realiza un movimiento rectilíneo.

la aceleración de un cuerpo puede descomponerse en sus componentes radial

\scriptstyle a_{r}

y tangencial

\scriptstyle a_{\theta }

, quedando:

${\begin{cases}a_{r}=a_{r}^{(0)}+a_{r}^{(cen)}={\cfrac {d^{2}r}{dt^{2}}}-r\left({\cfrac {d\theta }{dt}}\right)^{2}={\cfrac {d^{2}r}{dt^{2}}}-r\omega ^{2}\\a_{\theta }=a_{\theta }^{(0)}+a_{\theta }^{(cor)}=r{\cfrac {d^{2}\theta }{dt^{2}}}+2{\cfrac {dr}{dt}}{\cfrac {d\theta }{dt}}=r\alpha +2{\cfrac {dr}{dt}}\omega \end{cases}}$

Donde: r y θ son las coordenadas polares de la partícula; ω es la velocidad angular (que es igual a dθ/dt); α es la aceleración angular (que es igual a dω/dt).

Se le llama aceleración centrípeta al término rω² presente en la componente radial de la aceleración a_r. Dado que v = ωr, la aceleración centrípeta también se puede escribir como:

$|a_{r}^{(cen)}|={\frac {v^{2}}{r}}=r\omega ^{2}$

El término 2(dr/dt)ω localizado en la componente tangencial de la aceleración es conocido como la aceleración de Coriolis.

En el movimiento circunferencial, mientras la dirección del vector velocidad va variando punto a punto, la aceleración centrípeta se manifiesta como un vector con origen en el vector posición y con dirección hacia el centro de la circunferencia.

VELOCIDAD ANGULAR OMEGA (W)

Para tener una idea de la rápidez con la que algo se està moviendo con movimiento circular, ellos definen la velocidad angular w como el número de vueltas que da el cuerpo por unidad de tiempo. si un cuerpo tiene gran velocidad angular quiere decir que da muchas vueltas por segundo. resumiendo: la velocidad es el movimiento circular es la cantidad de vueltas que un cuerpo da por segundo.
Velocidad angular:
w=α/t

una misma velocidad angular se puede poner de varias maneras. por ejemplo, para la lavarropas o para los motores de los autos se usan las revoluciones por minuto. Tambièn a veces se usan las RPS. tambièn los grados por segundo, es decir, hay muchas unidades diferentes de velocidad angular. todos se usan y hay que saber pasar de una a otra. no es muy complicado el pasaje, solo se hacen reglas de 3 muy simples.

la mas importane de todas las unidades de velocidad angular es la de radianes por segundo. El radian es un numero sinunidad y sin palabra, no suele ponerse.

Condiciones de Equilibrio

CONDICIONES DE EQUILIBRIO

Las condiciones de equilibrio son las leyes que rigen la estática. La estática es la ciencia que estudia las fuerzas que se aplican a un cuerpo para describir un sistema en equilibrio. Diremos que un sistema está en equilibrio cuando los cuerpos que lo forman están en reposo, es decir, sin movimiento. Las fuerzas que se aplican sobre un cuerpo pueden ser de tres formas:
-Fuerzas angulares: Dos fuerzas se dice que son angulares, cuando actúan sobre un mismo punto formando un ángulo.

-Fuerzas colineales: Dos fuerzas son colineales cuando la recta de acción es la misma, aunque las fuerzas pueden estar en la misma dirección o en direcciones opuestas.

-Fuerzas paralelas: Dos fuerzas son paralelas cuando sus direcciones son paralelas, es decir, las rectas de acción son paralelas, pudiendo también aplicarse en la misma dirección o en sentido contrario.

A nuestro alrededor podemos encontrar numerosos cuerpos que se encuentran en equilibrio. La explicación física para que esto ocurra se debe a las condiciones de equilibrio:

Primera condición de equilibrio: Diremos que un cuerpo se encuentra en equilibrio de traslación cuando la fuerza resultante de todas las fuerzas que actúan sobre él es nula: ∑ F = 0.
Desde el punto de vista matemático, en el caso de fuerzas coplanarias, se tiene que cumplir que la suma aritmética de las fuerzas o de sus componentes que están el la dirección positiva del eje X sea igual a las componentes de las que están en la dirección negativa. De forma análoga, la suma aritmética de las componentes que están en la dirección positiva del eje Y tiene que ser igual a las componentes que se encuentran en la dirección negativa:
Por otro lado, desde el punto de vista geométrico, se tiene que cumplir que las fuerzas que actúan sobre un cuerpo en equilibrio tienen un gráfico con forma de polígono cerrado; ya que en el gráfico de las fuerzas, el origen de cada fuerza se representa a partir del extremo de la fuerza anterior.

Segunda condición de equilibrio: Por otro lado, diremos que un cuerpo está en equilibrio de rotación cuando la suma de todas las fuerzas que se ejercen en él respecto a cualquier punto es nula. O dicho de otro modo, cuando la suma de los momentos de torsión es cero.

En este caso, desde el punto de vista matemático, y en el caso anterior en el que las fuerzas son coplanarias; se tiene que cumplir que la suma de los momentos o fuerzas asociados a las rotaciones antihorarias (en el sentido contrario de las agujas del reloj), tiene que ser igual a la suma aritmética de los momentos o fuerzas que están asociados a las rotaciones horarias (en el sentido de las agujas del reloj):

Un cuerpo se encuentra en equilibrio traslacional y rotacional cuando se verifiquen de forma simultánea las dos condiciones de equilibrio. Estas condiciones de equilibrio se convierten, gracias al álgebra vectorial, en un sistema de ecuaciones cuya solución será la solución de la condición del equilibrio.

Tercera Ley de Newton

TERCERA LEY DE NEWTON

La tercera ley de Newton establece que siempre que un objeto ejerce una fuerza sobre un segundo objeto, este ejerce una fuerza de igual magnitud y dirección pero en sentido opuesto sobre el primero. Con frecuencia se enuncia así: A cada acción siempre se opone una reacción igual pero de sentido contrario. En cualquier interacción hay un par de fuerzas de acción y reacción situadas en la misma dirección con igual magnitud y sentidos opuestos. La formulación original de Newton es:

Actioni contrariam semper & æqualem esse reactionem: sive corporum duorum actiones in se mutuo semper esse æquales & in partes contrarias dirigi.¹¹

Con toda acción ocurre siempre una reacción igual y contraria: quiere decir que las acciones mutuas de dos cuerpos siempre son iguales y dirigidas en sentido opuesto.¹³

Esta tercera ley de Newton es completamente original (pues las dos primeras ya habían sido propuestas de otra manera por Galileo, Hooke y Huygens) y hace de las leyes de la mecánica un conjunto lógico y completo.¹⁹ Expone que por cada fuerza que actúa sobre un cuerpo, este realiza una fuerza de igual intensidad, pero de sentido contrario sobre el cuerpo que la produjo. Dicho de otra forma, las fuerzas, situadas sobre la misma recta, siempre se presentan en pares de igual magnitud y de dirección, pero con sentido opuesto. Si dos objetos interaccionan, la fuerza F₁₂, ejercida por el objeto 1 sobre el objeto 2, es igual en magnitud con misma dirección pero sentidos opuestos a la fuerza F₂₁ ejercida por el objeto 2 sobre el objeto 1:²⁰

\mathbf {F} _{12}=-\mathbf {F} _{21}

Este principio presupone que la interacción entre dos partículas se propaga instantáneamente en el espacio (lo cual requeriría velocidad infinita), y en su formulación original no es válido para fuerzas electromagnéticas puesto que estas no se propagan por el espacio de modo instantáneo sino que lo hacen a velocidad finita "c". Este principio relaciona dos fuerzas que no están aplicadas al mismo cuerpo, produciendo en ellos aceleraciones diferentes, según sean sus masas. Por lo demás, cada una de esas fuerzas obedece por separado a la segunda ley. Junto con las anteriores leyes, esta permite enunciar los principios de conservación del momento lineal y del momento angular.

Aplicaciones de la Tercera Ley de Newton

Algunos ejemplos donde actúan las fuerzas acción-reacción son los siguientes:

Si una persona empuja a otra de peso similar, las dos se mueven con la misma velocidad pero en sentido contrario.
Cuando saltamos, empujamos a la tierra hacia abajo, que no se mueve debido a su gran masa, y esta nos empuja con la misma intensidad hacia arriba.
Una persona que rema en un bote empuja el agua con el remo en un sentido y el agua responde empujando el bote en sentido opuesto.
Cuando caminamos empujamos a la tierra hacia atrás con nuestros pies, a lo que la tierra responde empujándonos a nosotros hacia delante, haciendo que avancemos.
Cuando se dispara una bala, la explosión de la pólvora ejerce una fuerza sobre la pistola (que es el retroceso que sufren las armas de fuego al ser disparadas), la cual reacciona ejerciendo una fuerza de igual intensidad pero en sentido contrario sobre la bala.
La fuerza de reacción que una superficie ejerce sobre un objeto apoyado en ella, llamada fuerza normal con dirección perpendicular a la superficie.

Segunda Ley de Newton

Esta ley se encarga de cuantificar el concepto de fuerza. La aceleración que adquiere un cuerpo es proporcional a la fuerza neta aplicada sobre el mismo. La constante de proporcionalidad es la masa del cuerpo (que puede ser o no ser constante). Entender la fuerza como la causa del cambio de movimiento y la proporcionalidad entre la fuerza impresa y el cambio de la velocidad de un cuerpo es la esencia de esta segunda ley.¹⁴

Si la masa es constante[editar]

Si la masa del cuerpo es constante se puede establecer la siguiente relación, que constituye la ecuación fundamental de la dinámica:

$\mathbf {F} _{\rm {resultante}}=m\mathbf {a}$

La aceleración que adquiere un cuerpo es proporcional a la fuerza aplicada, y la constante de proporcionalidad es la masa del cuerpo.
Si actúan varias fuerzas, esta ecuación se refiere a la fuerza resultante, suma vectorial de todas ellas.
Esta es una ecuación vectorial, luego se debe cumplir componente a componente.
En ocasiones será útil recordar el concepto de componentes intrínsecas: si la trayectoria no es rectilínea es porque hay una aceleración normal, luego habrá también una fuerza normal (en dirección perpendicular a la trayectoria); si el módulo de la velocidad varía es porque hay una aceleración en la dirección de la velocidad (en la misma dirección de la trayectoria).
La fuerza y la aceleración son vectores paralelos, pero esto no significa que el vector velocidad sea paralelo a la fuerza. Es decir, la trayectoria no tiene por qué ser tangente a la fuerza aplicada (sólo ocurre si al menos, la dirección de la velocidad es constante).
Esta ecuación debe cumplirse para todos los cuerpos. Cuando analicemos un problema con varios cuerpos y diferentes fuerzas aplicadas sobre ellos, deberemos entonces tener en cuenta las fuerzas que actúan sobre cada uno de ellos y el principio de superposición de fuerzas. Aplicaremos la segunda ley de Newton para cada uno de ellos, teniendo en cuenta las interacciones mutuas y obteniendo la fuerza resultante sobre cada uno de ellos.
El principio de superposición establece que si varias fuerzas actúan igual o simultáneamente sobre un cuerpo, la fuerza resultante es igual a la suma vectorial de las fuerzas que actúan independientemente sobre el cuerpo (regla del paralelogramo). Este principio aparece incluido en los Principia de Newton como Corolario 1, después de la tercera ley, pero es requisito indispensable para la comprensión y aplicación de las leyes, así como para la caracterización vectorial de las fuerzas.¹⁴ La fuerza modificará el estado de movimiento, cambiando la velocidad en módulo o dirección. Las fuerzas son causas que producen aceleraciones en los cuerpos. Por lo tanto existe una relación causa-efecto entre la fuerza aplicada y la aceleración que se este cuerpo experimenta.

De esta ecuación se obtiene la unidad de medida de la fuerza en el Sistema Internacional de Unidades, el Newton:

${\rm {1\,N=1\;{{kg\cdot m} \over s^{2}}}}$

Por otra parte, si la fuerza resultante que actúa sobre una partícula no es cero, esta partícula tendrá una aceleración proporcional a la magnitud de la resultante y en dirección de esta (debido a que la masa siempre es un escalar positivo). La expresión anterior así establecida es válida tanto para la mecánica clásica como para la mecánica relativista.

Si la masa no es constante[editar]

Si la masa de los cuerpos varía, como por ejemplo un cohete que va quemando combustible, no es válida la relación $\mathbf {F} =m\mathbf {a}$ y hay que hacer genérica la ley para que incluya el caso de sistemas en los que pueda variar la masa. Para ello primero hay que definir una magnitud física nueva, la cantidad de movimiento, que se representa por la letra p y que se define como el producto de la masa de un cuerpo por su velocidad, es decir:

$\mathbf {p} =m\mathbf {v}$

Newton enunció su ley de una forma más general:

$\mathbf {F} _{\rm {neta}}={\frac {\mathrm {d} (m\mathbf {v} )}{\mathrm {d} t}}$

De esta forma se puede relacionar la fuerza con la aceleración y con la masa, sin importar que esta sea o no sea constante. Cuando la masa es constante sale de la derivada con lo que queda la expresión:

$\mathbf {F} _{\rm {neta}}=m\,{\frac {\mathrm {d} \mathbf {v} }{\mathrm {d} t}}$

Y se obtiene la expresión clásica de la Segunda Ley de Newton:

$\mathbf {F} _{\rm {neta}}=m\mathbf {a}$

La fuerza, por lo tanto, es un concepto matemático el cual, por definición, es igual a la derivada con respecto al tiempo del momento de una partícula dada, cuyo valor a su vez depende de su interacción con otras partículas. Por consiguiente, se puede considerar la fuerza como la expresión de una interacción. Otra consecuencia de expresar la Segunda Ley de Newton usando la cantidad de movimiento es lo que se conoce como principio de conservación de la cantidad de movimiento: si la fuerza total que actúa sobre un cuerpo es cero, la Segunda ley de Newton nos dice que

$0={\frac {\mathrm {d} \mathbf {p} }{\mathrm {d} t}}$

Es decir, la derivada de la cantidad de movimiento con respecto al tiempo es cero en sus tres componentes. Esto significa que la cantidad de movimiento debe ser constante en el tiempo en módulo dirección y sentido (la derivada de un vector constante es cero).

Primera Ley de Newton

PRIMERA LEY DE NEWTON

La primera ley de Newton, establece que un objeto permanecerá en reposo o con movimiento uniforme rectilíneo al menos que sobre él actúe una fuerza externa. Puede verse como un enunciado de la ley de inercia, en que los objetos permanecerán en su estado de movimiento cuando no actuan fuerzas externas sobre el mismo para cambiar su movimiento.
La primera ley de Newton, contiene implicaciones sobre la simetría fundamental del Universo, en la que el estado de movimiento en línea recta debe considerarse tan natural como el estado de reposo. Si un objeto está en reposo respecto de una marco de referencia, aparecerá estar moviéndose en línea recta para un observador que se esté moviendo igualmente en línea recta respecto del objeto. No hay forma de saber que marco de referencia es especial, de modo que, todos los marcos de referencias de velocidad rectilínea constante son equivalentes.

Esta ley postula, por tanto, que un cuerpo no puede cambiar por sí solo su estado inicial, ya sea en reposo o en movimiento rectilíneo uniforme, a menos que se aplique una fuerza o una serie de fuerzas cuya resultante no sea nula. Newton toma en consideración, así, el que los cuerpos en movimiento están sometidos constantemente a fuerzas de roce o fricción, que los frena de forma progresiva, algo novedoso respecto de concepciones anteriores que entendían que el movimiento o la detención de un cuerpo se debía exclusivamente a si se ejercía sobre ellos una fuerza, pero nunca entendiendo como tal a la fricción.

En consecuencia, un cuerpo que se desplaza con movimiento rectilíneo uniforme implica que no existe ninguna fuerza externa neta o, dicho de otra forma, un objeto en movimiento no se detiene de forma natural si no se aplica una fuerza sobre él. En el caso de los cuerpos en reposo, se entiende que su velocidad es cero, por lo que si esta cambia es porque sobre ese cuerpo se ha ejercido una fuerza neta.

Newton retomó la ley de la inercia de Galileo: la tendencia de un objeto en movimiento a continuar moviéndose en una línea recta, a menos que sufra la influencia de algo que le desvíe de su camino. Newton supuso que si la Luna no salía disparada en línea recta, según una línea tangencial a su órbita, se debía a la presencia de otra fuerza que la empujaba en dirección a la Tierra, y que desviaba constantemente su camino convirtiéndolo en un círculo. Newton llamó a esta fuerza gravedad y creyó que actuaba a distancia. No hay nada que conecte físicamente la Tierra y la Luna y sin embargo la Tierra está constantemente tirando de la Luna hacia nosotros. Newton se sirvió de la tercera ley de Kepler y dedujo matemáticamente la naturaleza de la fuerza de la gravedad. Demostró que la misma fuerza que hacía caer una manzana sobre la Tierra mantenía a la Luna en su órbita.

La primera ley de Newton establece la equivalencia entre el estado de reposo y de movimiento rectilíneo uniforme. Supongamos un sistema de referencia S y otro S´ que se desplaza respecto del primero a una velocidad constante. Si sobre una partícula en reposo en el sistema S´ no actúa una fuerza neta, su estado de movimiento no cambiará y permanecerá en reposo respecto del sistema S´ y con movimiento rectilíneo uniforme respecto del sistema S. La primera ley de Newton se satisface en ambos sistemas de referencia. A estos sistemas en los que se satisfacen las leyes de Newton se les da el nombre de sistemas de referencia inerciales. Ningún sistema de referencia inercial tiene preferencia sobre otro sistema inercial, son equivalentes: este concepto constituye el principio de relatividad de Galileo o newtoniano.

La primera ley de Newton sirve para definir un tipo especial de sistemas de referencia conocidos como sistemas de referencia inerciales, que son aquellos desde los que se observa que un cuerpo sobre el que no actúa ninguna fuerza neta se mueve con velocidad constante.

Un sistema de referencia con aceleración (y la aceleración normal de un sistema rotatorio se incluye en esta definición) no es un sistema inercial, y la observación de una partícula en reposo en el propio sistema no satisfará las leyes de Newton (puesto que se observará aceleración sin la presencia de fuerza neta alguna). Se denominan sistemas de referencia no inerciales.