MRUA

Encontrar el movimiento rectilíneo uniformemente acelerado (m.r.u.a.) o movimiento rectilíneo uniformemente variado (m.r.u.v.) en tu día a día es bastante común. Por ejemplo, si dejas caer una moneda al suelo (caida libre), esta realizará un movimiento rectilíneo uniformemente acelerado (m.r.u.a.) omovimiento rectilíneo uniformemente variado (m.r.u.v.). En este apartado vamos a estudiar las ecuaciones y las gráficas que definen a este movimiento.

Un cuerpo realiza un movimiento rectilíneo uniformemente acelerado (m.r.u.a.) omovimiento rectilíneo uniformemente variado (m.r.u.v.)cuando su trayectoria es una línea recta y su aceleración es constante. Esto implica que la velocidad aumenta o disminuye su módulo de manera uniforme.

A la aceleración responsable de que cambie el módulo de la velocidad (también llamado celeridad o rapidez), se le denomina aceleración tangencial.

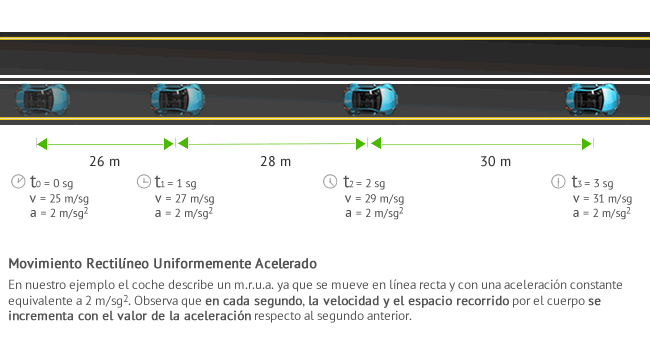
Ecuaciones y Gráficas del M.R.U.A.

Velocidad

Su unidad en el Sistema Internacional (S.I.) es el metro por segundo (m/s). Cambia de manera uniforme y se obtiene por medio de la siguiente expresión:

v=v0+a⋅t

donde:

• v₀ es la velocidad inicial.
• a es la aceleración que tiene el cuerpo.
• t es el intervalo de tiempo en el que se estudia el movimiento.

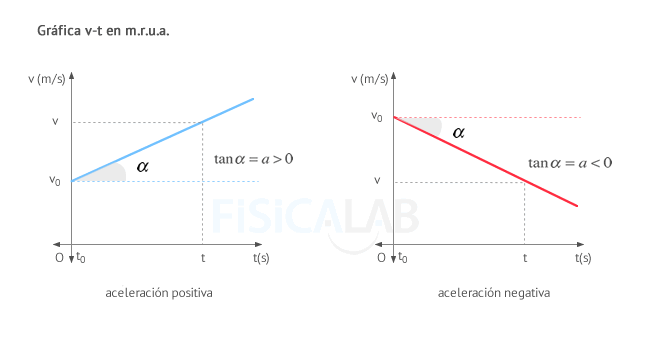
 A mayor pendiente, mayor es la aceleración del cuerpo.

Posición

Su unidad en el Sistema Internacional (S.I.) es el metro (m) y se calcula mediante la siguiente expresión:

x=x0+v0t+12at2

donde:

• x₀ es las posición inicial.
• v₀ es la velocidad inicial.
• a es la aceleración.
• t es el intervalo de tiempo en el que se estudia el movimiento.

Gráficamente se trata de una parábola donde x₀ representa la posición inicial del cuerpo y a la aceleración del mismo.

Aceleración

Su unidad en el Sistema Internacional (S.I.) es el metro por segundo al cuadrado (m/s²). Su valor permanece constante y distinto de 0.

a=cte

Cuando:

• a>0, la velocidad aumenta su valor y se dice que el cuerpo está acelerando.
• a<0, la velocidad disminuye su valor y se dice que el cuerpo está frenando.

Observa lo que t representa en las ecuaciones anteriores: El intervalo de tiempo durante el cual se mueve el cuerpo. Dicho intervalo a veces es representado por t y otras por ∆t. En cualquier caso t=∆t = t_f - t_i siendo t_f y t_ilos instantes de tiempo inicial y final respectivamente.

Por último, recuerda que, si consideras el eje vertical y, puedes encontrar la ecuación de posición anterior en la forma

y=y0+v0t+12at2

Ejemplo

Un motorista que circula a 50 Km/h, sigue una trayectoria rectilínea hasta que acciona los frenos de su vehículo y se detiene completamente. Si desde que frena hasta que se para transcurren 6 segundos, calcula:

a) La aceleración durante la frenada.
b) La velocidad con que se movía transcurridos 3 segundos desde que comenzó a frenar.
c) En que instante, desde que comenzó a frenar su velocidad fué de 1 m/s.

Ver solución